MAIN RESEARCH PROJECTS

STATISTICAL PHYSICS, COMPUTATIONAL AND SYSTEMS BIOLOGY
Machine Learning the impact of Genomic Variants (PRISMR)Genome Architecture Mapping (GAM) technology
Polymer physics of chromatin 3D organization (SBS model)
Higher-order chromatin structures (metaTADs)
Symmetry Breaking of Olfactory Receptors, and XCI
Network of single-cell states in cell transition processes
Statistical Mechanics of Complex Systems in Physics
Statistical Mechanics of Granular MediaRheology of Granular Media
STATISTICAL PHYSICS, COMPUTATIONAL AND SYSTEMS BIOLOGY
Machine Learning the impact of Genomic Variants (PRISMR)
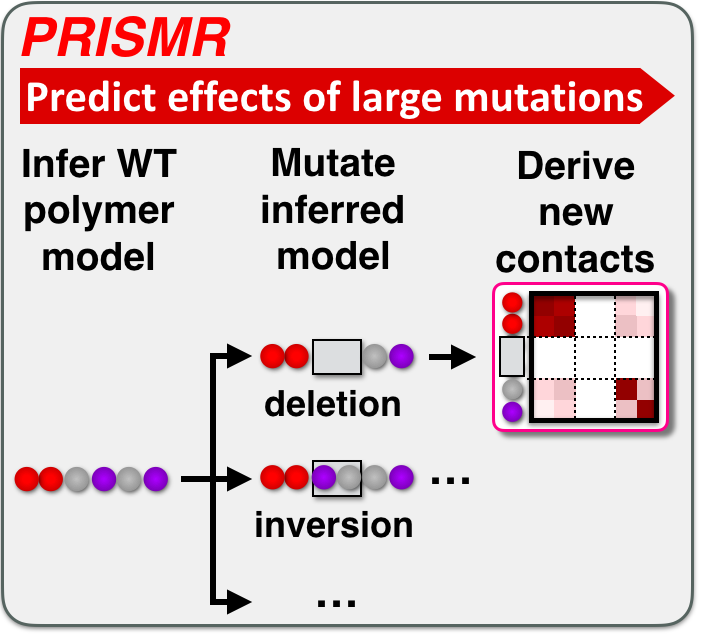
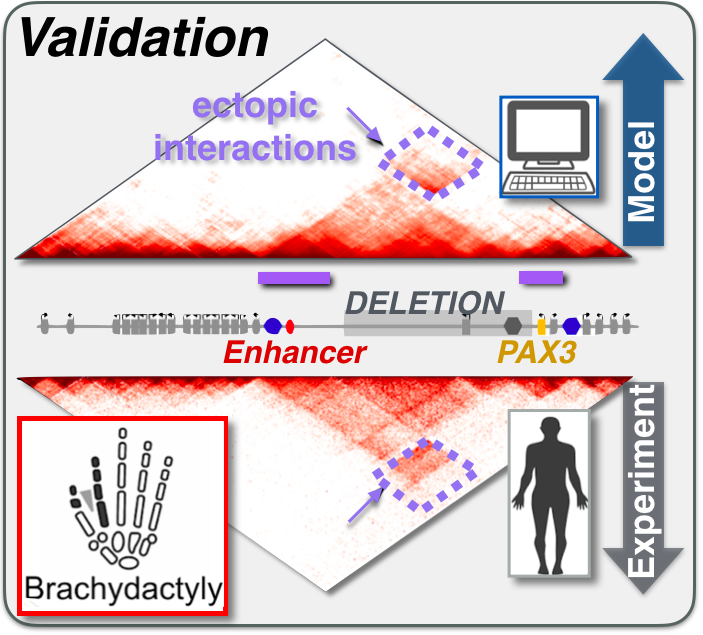
Large genomic mutations (Structural Variants, SVs) can change the activity of genes by altering their contact network with enhancers. Linked to diseases such as congenital disorders or cancer, their effects remain difficult to predict. We developed PRISMR, a method combining Machine Learning and Polymer Physics, to model 3D chromatin folding. Trained on wild-type data, upon a mutation it successfully predicts how chromatin refolds, and enhancer-promoter contacts rewire. Validated across mutations in mice and human cells, PRISMR can reveal disease-causing potential and involved molecular factors of SVs genome-wide in single individuals.
Selected references:
B.K. Kragesteen, et al., "Dynamic 3D chromatin architecture contributes to enhancer specificity and limb morphogenesis", Nature Genetics 50, 1463 (2018)
S. Bianco et al., "Polymer Physics Predicts the Effects of Structural Variants on Chromatin Architecture", Nature Genetics 50, 662 (2018)
Genome Architecture Mapping (GAM) technology
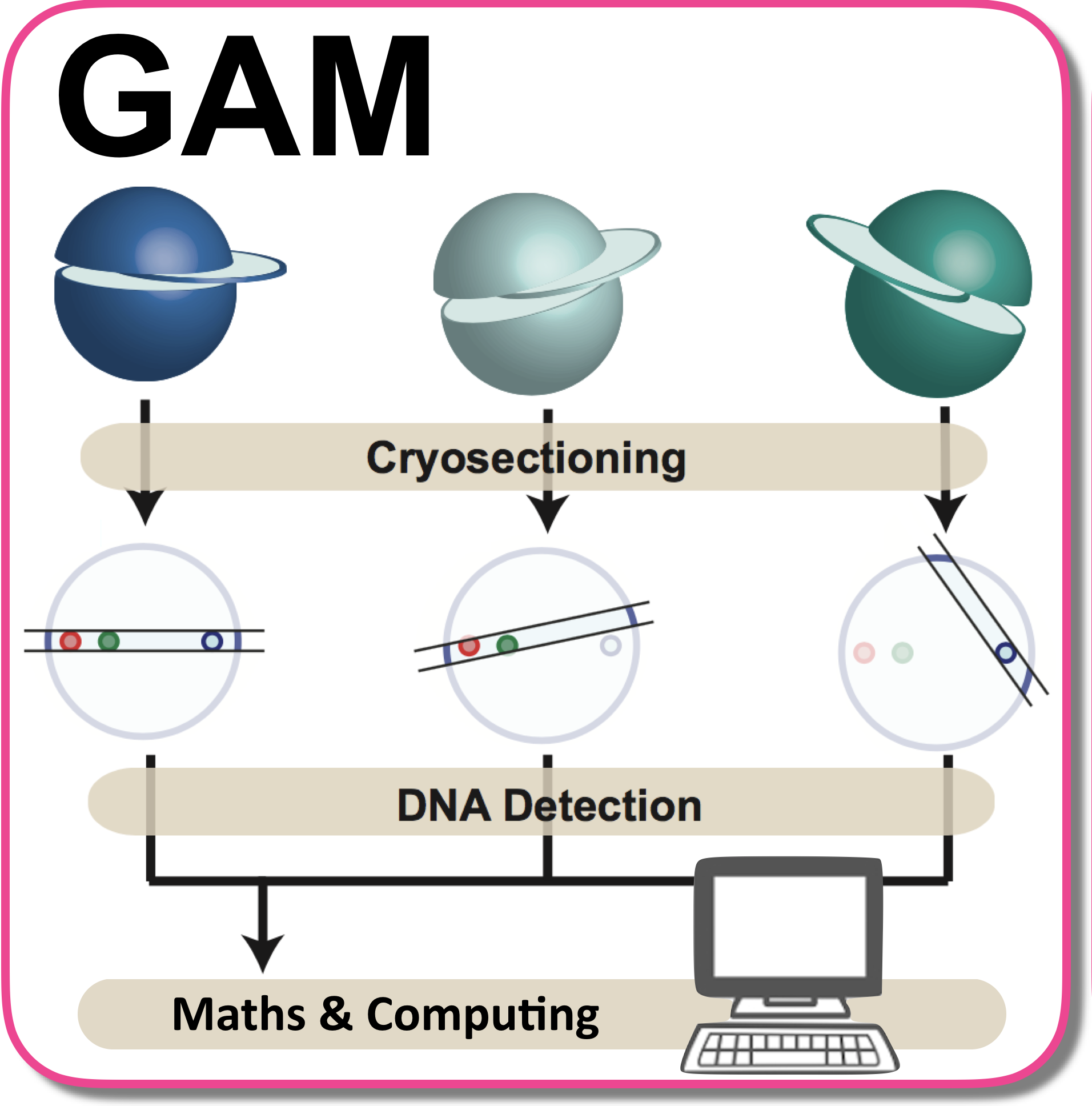
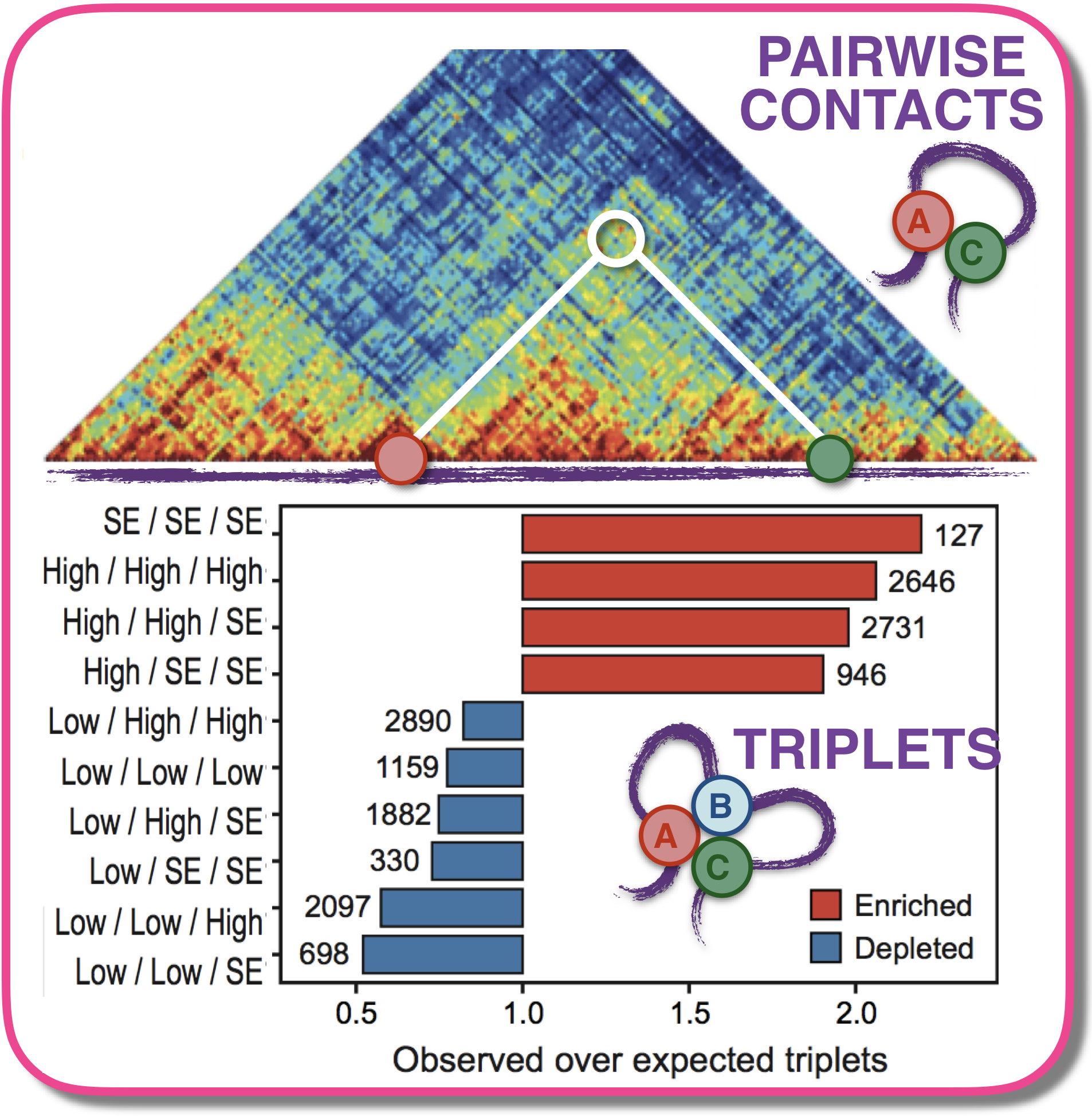
Genome Architecture Mapping (GAM) is a ligation-free technology to map genome-wide chromosome interactions, beyond pairwise contacts, alternative to Hi-C methods. Developed in collaboration with A. Pombo, its concept is simple: in slices extracted from the cell nucleus, spatially closer sites are found to co-segregate more frequently, and maths can dissect real contacts from random encounters. We find, for instance, that highly transcribed regions or super-enhancers tend to form more frequently three-way or multiple contacts. We also investigated how faithful Hi-C, SPRITE and GAM technologies are to the 3D structure of chromatin and how they perform relative to each other.
Selected references:
R.A. Beagrie et al., "Multiplex-GAM: genome-wide identification of chromatin contacts yields insights overlooked by Hi-C" , Nature Meth. 20, 1037 (2023)
W. Winick-Ng et al., "Cell-type specialization is encoded by specific chromatin topologies", Nature 599, 684 (2021)
L. Fiorillo et al., "Comparison of the Hi-C, GAM and SPRITE methods using polymer models of chromatin", Nature Methods 18, 482 (2021)
R.A. Beagrie et al., "Complex multi-enhancer contacts captured by genome architecture mapping", Nature 543, 519 (2017)
Polymer physics of chromatin 3D organization (SBS model)
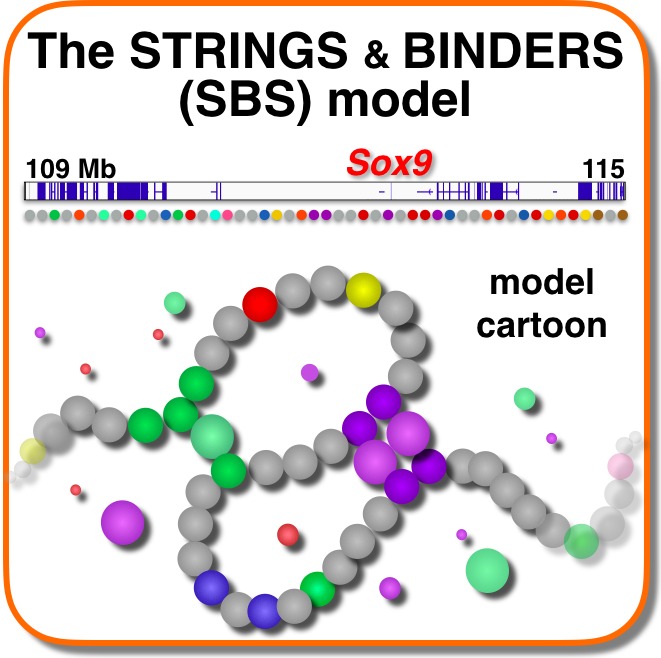
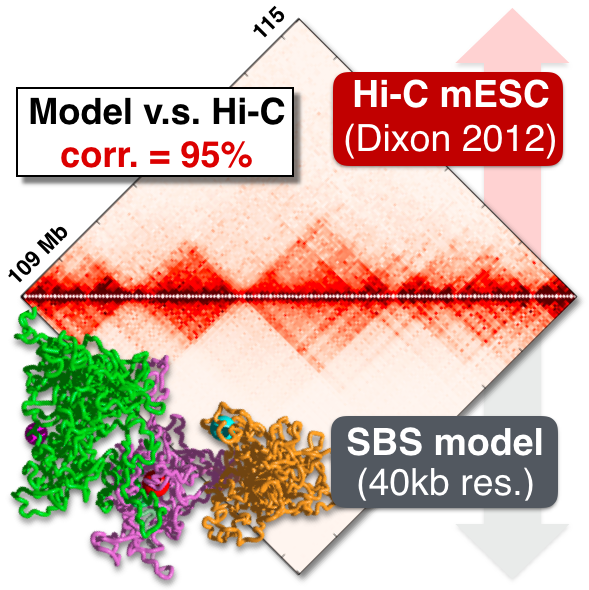
We use principled models from physics to investigate the mechanisms shaping chromosome 3D organisation and its functional role. Our Strings&Binders (SBS) model represents the scenario where binding molecules produce contacts between distal DNA sites, such as genes and their regulators. It explains Hi-C, SPRITE, GAM and super-resolution microscopy data at the single-molecule level, via mechanisms of polymer phase separation. It finds that chromosome architecture is shaped by the combinatorial action of different molecular factors, such as Pol-II, PRC2, CTCF, cohesin or RNAs. For example, cohesin depletion reverses phase separation into a random coil state, erasing average interaction patterns. Model predictions on the effects of genomic factors and rearrangements are experimentally confirmed, opening to new tools to attack diseases linked to chromatin misfolding, such as congenital disorders and cancer.
Selected references:
M. Conte et al., "Loop-extrusion and polymer phase-separation can co-exist at the single-molecule level to shape chromatin folding" , Nature Com. 13, 4070 (2022)
M. Conte et al., "Polymer physics indicates chromatin folding variability across single-cells results from state degeneracy in phase-separation" , Nature Com. 11, 3289 (2020)
M. Barbieri et al., "Active and poised promoter states drive folding of the extended HoxB locus in mouse embryonic stem cells" , Nature Struct. Mol. Bio. 24, 515 (2017)
A.M. Chiariello et al., "Polymer physics of chromosome large-scale 3D organisation", Nature Scientific Reports 6, 29775 (2016)
M. Barbieri et al., "Complexity of chromatin folding is captured by the
strings and binders switch model" , PNAS
109, 16173 (2012)
M. Nicodemi et al., "Thermodynamic pathways to genome spatial organization in the cell nucleus" , Biophys.Jou. 96, 2168 (2009)
Higher-order chromatin structures (metaTADs)
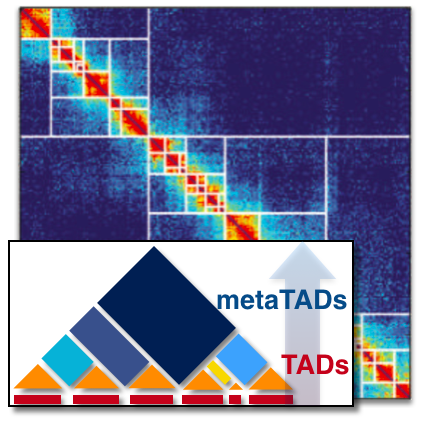
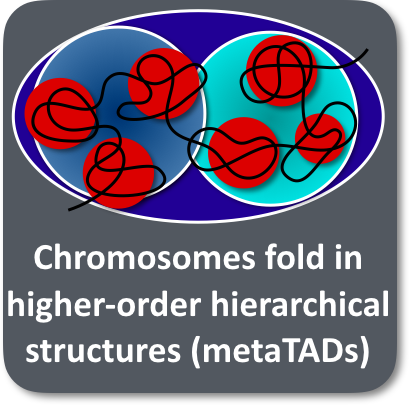
Genome-wide mapping of chromatin architecture in mouse and human cells reveals a hierarchical 3D organization of chromatin in higher-order domains (metaTADs) extending across chromosomal scales. The topology of MetaTAD reflects epigenomic features and is only relatively conserved, for example, through neuronal differentiation, while its rewiring relates to changes in gene expression. The molecular mechanisms of metaTAD self-assembly are well explained by microphase separation within the SBS polymer model.
Selected references:
J. Fraser et al., "Hierarchical folding and reorganization of chromosomes are linked to transcriptional changes during cellular differentiation", Mol. Sys. Bio. 11, 852 (2015)
A. Pombo and M. Nicodemi, "Models of chromosome structure", Curr. Opin. Cell Bio. 28, 90 (2014)
Symmetry Breaking of Olfactory Receptors, and XCI
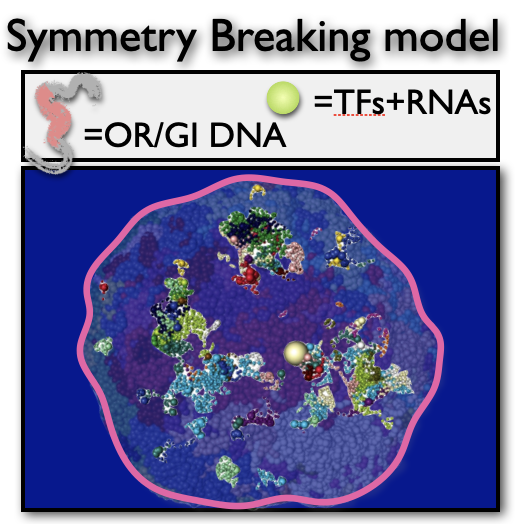
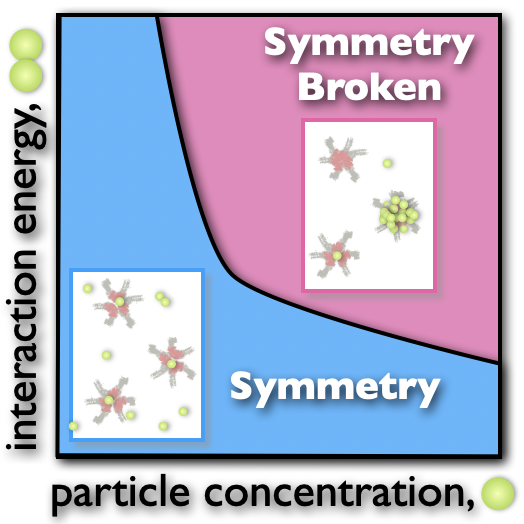
In mammals, each olfactory neuron expresses only one, randomly chosen allele out of 1000 equivalent olfactory receptor (OR) genes, while the others are silenced in a surprisingly precise, yet stochastic regulatory process. With S. Lomvardas we identified the underlying Symmetry Breaking (SB) mechanism: a set of interacting molecules, encompassing OR Transcription Factors and RNAs, phase separate into a single enhancer hub including the future active OR. SB mechanisms could also control X-Chromosome Inactivation (XCI), the process in female embryos whereby each cell inactivates one, randomly selected X to equalise X products w.r.t. males. The SB scenario where a set of X-linked molecules form a single 'X blocking factor' is consistent with current experiments.
Selected references:
A.D. Pourmorady, E.V. Bashkirova, A.M. Chiariello et al., "RNA-mediated symmetry breaking enables singular olfactory receptor choice" ,
Nature 625, 181 (2024)
M. Nicodemi and A. Prisco, "A Symmetry Breaking Model for X Chromosome Inactivation", Phys. Rev. Lett. 98, 108104 (2007)
Network of single-cell states in cell transition processes
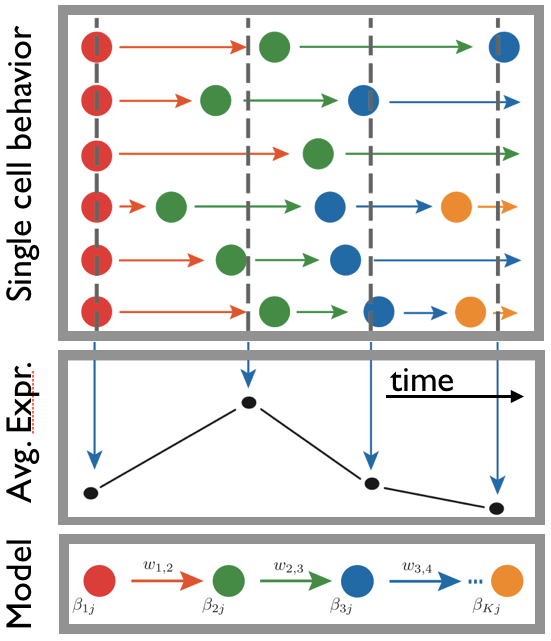
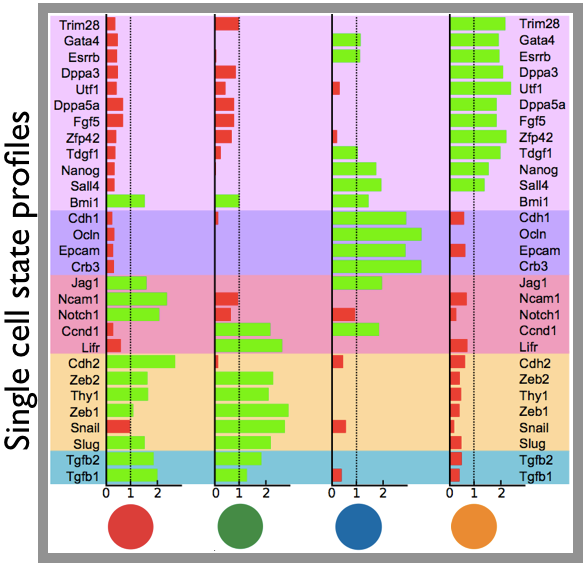
Differentiation, reprogramming and disease transformations involve transitions of cells through distinct states. Yet, accessing the key properties of such single-cell states can be extremely challenging. We introduced a stochastic model where the dynamics of a cell is described as a sequence of transitions in a network of states. By fitting genome-wide time-course data, the network of states, their transition rates and profiles can be reconstructed. The state structure predicted by our approach, e.g., in MEF reprogramming to pluripotency or in CD4+ T-cell differentiation, was supported by independent single-cell experiments.
Selected references:
V. Proserpio, et al. "Single-cell analysis of CD4+ T-cell differentiation reveals three major cell states and progressive acceleration of proliferation", Genome Biology 17, 103 (2016)
J.W. Armond, et al. "A stochastic model dissects cell states in biological transition processes", Nature Scientific Reports 4, 3692 (2014)
STATISTICAL MECHANICS OF COMPLEX SYSTEMS IN PHYSICS
Statistical Mechanics of Granular Media
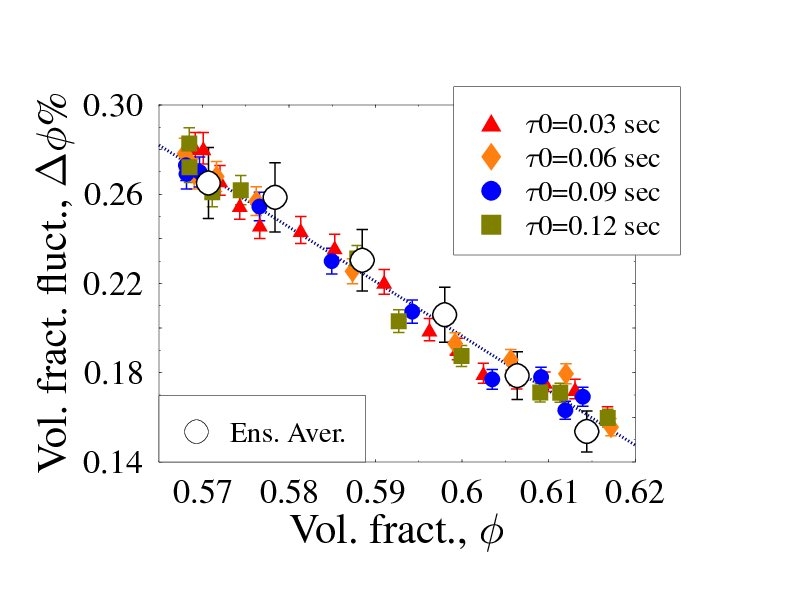
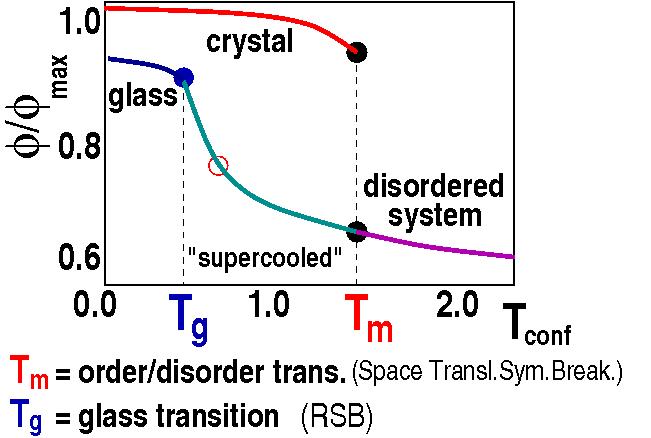
Granular media are the second most dealt with material in human activities after water. As they are non-thermal systems (can have zero kinetic energy at room temperature), standard thermodynamics does not apply and a first principles theory for their description is still missing. We showed that they can be described via a generalized Statistical Mechanics approach via suitable ensemble averages (with an effective thermodynamic parameter, T), and derived the system phase diagram. That's confirmed by recent experiments and computer simulations.
Selected references:
M. Pica Ciamarra, A. Coniglio, and M. Nicodemi,"Thermodynamics and Statistical Mechanics of Dense Granular Media", Phys. Rev. Lett. 97, 158001 (2006)
P. Richard, M. Nicodemi, R. Delannay, P. Ribiere, D. Bideau, "Slow
relaxation and compaction of granular systems", Nature
Materials 4, 121 (2005)
M. Nicodemi, "Dynamical response functions in models of vibrated granular media", Phys. Rev. Lett. 82, 3734 (1999)
Rheology of Granular Media
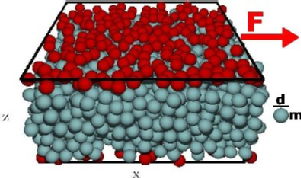
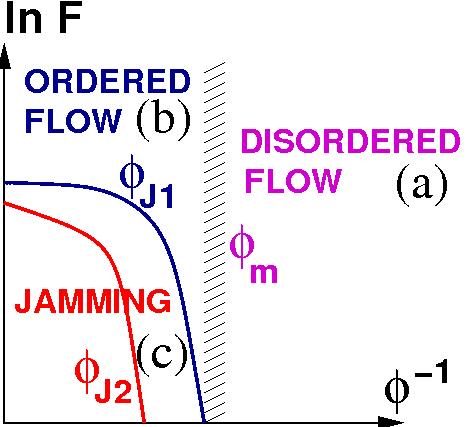
The rheology of non-thermal systems such as granular suspensions is currently focus of intense research for both fundamental science and practical applications. We explored the nature of the system flow diagram and found that its different regimes are separated by sharp, yet stochastic transitions: (a) disordered grain flow, (b) ordered grain flow and (c) grain jamming. We discovered that disordered flow has an Ostwald-de Waele-type power-law shear-stress constitutive relation, while a nearly solid plug appears in ordered flow.
Selected references:
D.S. Grebenkov, M. Pica Ciamarra, M. Nicodemi, A. Coniglio, "Flow,
ordering, and jamming of sheared granular suspensions" , Phys.Rev. Lett. 100, 078001 (2008)
M. Pica Ciamarra, A. Coniglio, and M. Nicodemi,"Shear instabilities in granular mixtures", Phys. Rev. Lett. 94, 188001 (2005)
M. Nicodemi,"Force correlations and arches formation in granular assemblies", Phys. Rev. Lett. 80, 1340 (1998)